摘要:本文介绍了最新面积公式及其应用。该公式可用于计算各种形状的面积,包括圆形、矩形、三角形等。该公式简单易用,计算精度高,广泛应用于数学、物理、工程等领域。通过实例演示,展示了该公式在实际问题中的应用方法和效果,为相关领域的研究和应用提供了有力的工具支持。
本文目录导读:
在几何学中,面积公式是计算图形面积的重要工具,随着科学技术的发展,传统的面积公式已经不能满足现代数学、物理、工程等领域的需求,研究人员不断探索新的面积公式,以解决实际问题,本文将介绍最新面积公式及其应用领域。
最新面积公式概述
最新面积公式是一种基于积分和微分技术的公式,适用于计算各种图形的面积,该公式具有普适性强、计算精度高、适用范围广等特点,与传统面积公式相比,最新面积公式能够更好地处理复杂图形的面积计算问题。
最新面积公式的推导
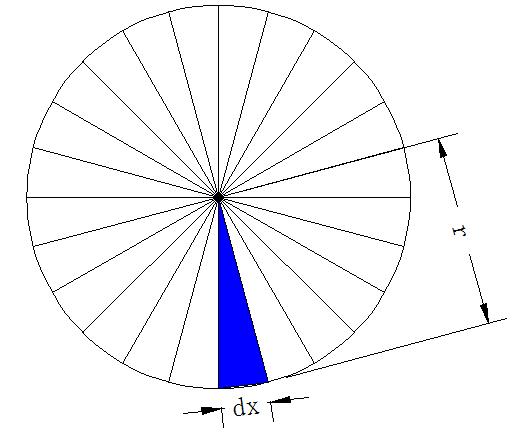
最新面积公式的推导基于微积分的基本原理,在二维平面上,任何不规则图形的面积都可以被近似地表示为一系列小矩形的面积之和,通过对这些小矩形的面积进行积分,我们可以得到图形的精确面积,具体推导过程如下:
假设图形在平面上的函数表示为y=f(x),在区间[a,b]上有定义,则图形的面积A可以通过以下公式计算:
A = ∫f(x)dx (从a到b)
这个公式即为最新面积公式的核心,通过选择不同的函数f(x)和区间[a,b],我们可以计算各种图形的面积。
最新面积公式的应用
最新面积公式在数学、物理、工程等领域有广泛的应用,以下是几个典型的应用实例:
1、数学领域:最新面积公式可用于计算曲线图形(如圆、椭圆、抛物线等)的面积,通过选择合适的函数和区间,可以精确地计算出这些图形的面积。
2、物理领域:在物理学中,最新面积公式被广泛应用于计算物理现象所涉及的面积,在计算电磁场、热传导等问题时,需要计算不规则图形的面积,最新面积公式可以提供精确的解决方案。
3、工程领域:工程师在设计和分析建筑结构、电路、流体动力学等问题时,需要计算各种图形的面积,最新面积公式可以帮助工程师快速、准确地完成这些计算,从而提高设计效率和准确性。
4、生物学和医学领域:生物学家和医学家在研究细胞结构、生物组织形态等问题时,需要计算不规则图形的面积,最新面积公式可以为其提供有效的计算工具,有助于揭示生物结构和功能的关系。
5、计算机科学领域:在计算机图形学、图像处理等领域,最新面积公式也被广泛应用,在计算图像中物体的面积、进行图像分割等任务时,最新面积公式可以提高计算精度和效率。
最新面积公式的优势与局限性
最新面积公式的优势主要表现在以下几个方面:
1、普适性强:最新面积公式适用于计算各种图形的面积,具有广泛的适用范围。
2、计算精度高:基于微积分原理,最新面积公式能够提供高精度的计算结果。
3、便于应用:最新面积公式在数学、物理、工程等领域都有广泛的应用,为解决实际问题提供了有力工具。
最新面积公式也存在一定的局限性:
1、复杂性:最新面积公式的推导和计算过程相对复杂,需要较高的数学基础。
2、计算量较大:对于复杂图形,最新面积公式的计算量较大,可能需要借助计算机进行辅助计算。
最新面积公式是一种基于微积分原理的面积计算公式,具有普适性强、计算精度高、适用范围广等特点,本文介绍了最新面积公式的基本原理、推导过程以及在数学、物理、工程等领域的应用,尽管最新面积公式存在一定的局限性,但随着科学技术的发展,其应用领域将会越来越广泛。

 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号